Límites laterales y continuidad: III. Continuidad
Ode navigation
 Loading viewer..
Loading viewer..
 Loading content..
Loading content..
756
Visitas
Ponlo en tu web
Ponlo en tu web
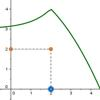
En esta actividad veremos qué significado tiene el límite de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.
Área de conocimiento
Tipo de recurso
Colecciones
Tipo de licencia
universal


Esta obra esta bajo una licencia" Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Usuario final
individual
Alumno en general
Alumno en general
Contexto educativo
Aula
Presencial
Contribuciones
publisher
INTEF
25/04/2024
publisher
INTEF
25/04/2024
author
Rafael Losada Liste
25/04/2024
publisher
Instituto Nacional de Tecnologías Educativas y Formación del Profesorado (INTEF)
25/04/2024
editor
Instituto Nacional de Tecnologías Educativas y Formación del Profesorado (INTEF)
25/04/2024
technical validator
Ángel Cabezudo Bueno
25/04/2024


