Teorema de Bolzano. Método de la bisección

Ode navigation

Hide navigation
View in full screen


Loading viewer.. Loading viewer..


Loading viewer.. Loading content..
234 Visitas
Ponlo en tu web

Ponlo en tu web

INTEF

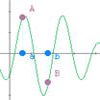
En esta escena Descartes, además de repasar el Teorema de Bolzano, se puede practicar el método de la bisección, basado en dicho teorema, para la aproximación de los puntos de corte con el eje OX de una función o, lo que es lo mismo, pra la aproximación sucesiva de raíces de una ecuación.

Área de conocimiento
Contexto educativo
Tipo de recurso
Colecciones
Tipo de licencia universal Licencia de Creative Commons
Esta obra esta bajo una licencia" Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Usuario final learner
Contribuciones
publisher INTEF 25/04/2024 publisher INTEF . 25/04/2024 publisher INTEF 25/04/2024 author Elena E. Álvarez Saiz 25/04/2024 publisher Instituto de Tecnologías Educativas (ITE) 25/04/2024 editor Instituto de Tecnologías Educativas (ITE) 25/04/2024 technical validator José María Aína Martínez 25/04/2024